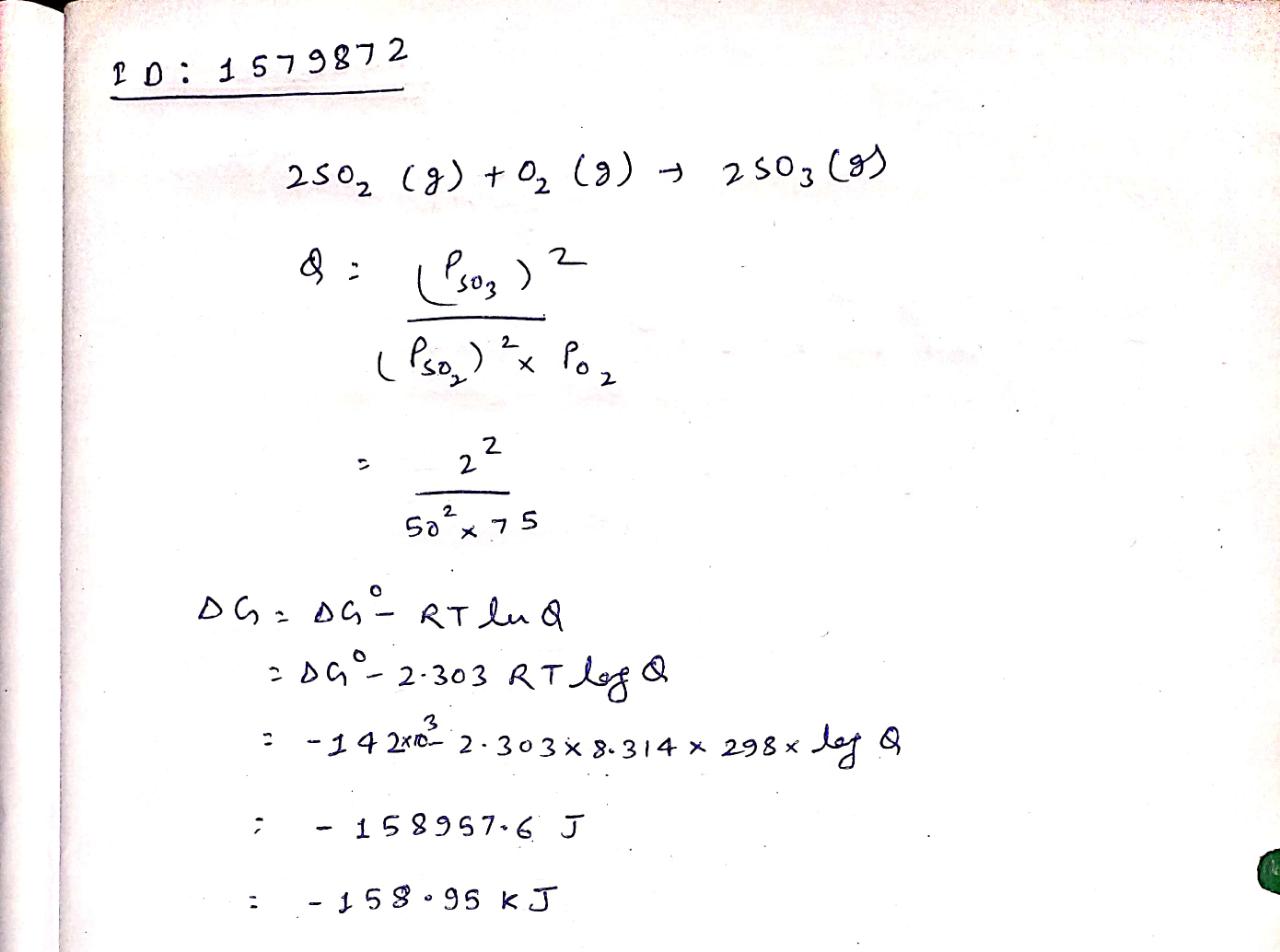Thermodynamics - Class 11 Medical Chemistry - Extra Questions
The standard heat of formation $$(\Delta_f H^0_{298})$$ of ethane (in kJ/mol), if the heat of combustion of ethane, hydrogen and graphite are $$-1560, -393.5 $$ and $$-286\ kJ/mol$$, respectively is ______.
The surface of copper gets tarnished by the formation of copper oxide. $$N_{2}$$ gets was passed to prevent the oxide formation during heating of copper at $$1250\ K$$. However, the $$N_{2}$$ gas contains $$1$$ mole % of water vapour as impurity. The water vapour oxidises copper as per the reaction given below:
$$2Cu(s) + H_{2}O(g) \rightarrow Cu_{2}O(s) + H_{2}(g)$$
$$\rho_{H_{2}}$$ is the minimum partial pressure of $$H_{2}$$ (in bar) needed to prevent the oxidation at $$1250\ K$$. The value of $$ln (\rho_{H_{2}})$$ is _________.
Given: Total pressure $$= 1\ bar$$$$R$$ (universal gas constant) $$= 8\ JK^{-1} mol^{-1}$$$$ ln (10) = 2.3$$$$Cu(s)$$ and $$Cu_{2}O(s)$$ are mutually immiscible
At $$1250\ K$$:$$2Cu(s) + 1/2O_{2}(g) \rightarrow Cu_{2}O(s); \ \Delta G^{\circ} = -78,000\ J\ mol^{-1}$$ $$H_{2}(g) + 1/2O_{2}(g) \rightarrow H_{2}O(g); \ \Delta G^{\circ} = -1,78,000\ J\ mol^{-1}$$[Upto one decimal point and take modulus of the answer]
Total pressure $$= 1\ bar$$
$$R$$ (universal gas constant) $$= 8\ JK^{-1} mol^{-1}$$
$$ ln (10) = 2.3$$
$$Cu(s)$$ and $$Cu_{2}O(s)$$ are mutually immiscible
At $$1250\ K$$:
At $$1250\ K$$:
$$2Cu(s) + 1/2O_{2}(g) \rightarrow Cu_{2}O(s); \ \Delta G^{\circ} = -78,000\ J\ mol^{-1}$$ $$H_{2}(g) + 1/2O_{2}(g) \rightarrow H_{2}O(g); \ \Delta G^{\circ} = -1,78,000\ J\ mol^{-1}$$
[Upto one decimal point and take modulus of the answer]
The degree of freedom of a three atomic molecule can not be 5. true=1, false=0
What is meant by an equilibrium?
The specific heat of a gas is 0.125 and 0.075 cal/g. The value of its molar mass is ______.
Thermochemical equations can be reversed by changing the sign of $$\Delta H$$.
If true enter 1, else enter 0.
If true enter 1, else enter 0.
$$\displaystyle \Delta G=\Delta H-T\Delta S$$.
If true enter 1, else enter 0.
If true enter 1, else enter 0.
Which has more heat capacity: a bucket full of water or a mug full of water?
Given equal masses of aluminium and copper, which would require more heat if both are heated to the same temperature. Justify your answer.
[Specific heat capacity of $$Al= 899 Jkg^{-1} C^{-1}$$ and $$Cu= 387 Jkg^{-1} C^{-1}$$]
Differentiate between heat capacity and specific heat capacity.
Why is water used as a coolant in car radiations and factories to keep the engine and other parts cool?
What is the quantity of heat released per kg of water per 1$$^o$$C fall in temperature?
Calculate the heat energy that will be released when 5.0 kg of steam at 100$$^o$$C condenses to form water at 100$$^o$$C. Express your answer in S.I. unit (specific heat of vapourisation of steam is 2268 kJ/kg)
Discuss the change in energy and arrangement of molecules on increasing the temperature of ice from -5$$^o$$C to 10$$^o$$C at 1 atm pressure.
Water falls from a height of 50 cm. Calculate the rise in temperature of water when it strikes the bottom. ($$g = 10 ms^{-2}$$, sp. heat capacity of water $$=4200 J/kg^oC$$)
Explain why
(a) Two bodies at different temperatures T$$\displaystyle _{1}$$ and T$$\displaystyle _{2}$$ if brought in thermal contact do not necessarily settle to the mean temperature (T$$\displaystyle _{1}$$ +T$$\displaystyle _{2}$$)/2
(b) The coolant in a chemical or a nuclear plant (i.e. the liquid used to prevent the different parts of a plant from getting too hot) should have high specific heat
(c) Air pressure in a car tyre increases during driving
(d) The climate of a harbour town is more temperate than that of a town in a desert at the same latitude
For the reaction,
2 A(g)+ B(g) $$ \displaystyle \rightarrow $$ 2D(g), $$ \displaystyle \bigtriangleup U^{\ominus }=-10.5KJ$$ and $$ \bigtriangleup S^{\ominus}=-44.1 JK^{-1} $$
Calculate $$ \displaystyle \bigtriangleup G^{\ominus } $$ for the reaction and predict whether the reaction may occur spontaneously.
Calculate $$ \displaystyle \bigtriangleup G^{\ominus } $$ for the reaction and predict whether the reaction may occur spontaneously.
State Hess's law of constant heat summation and explain it with an example.
State Hess's law.
$$1$$ mole of $${ Fe }_{ 2 }{ O }_{ 3 }$$ and $$2$$ moles of $$Al$$ are mixed at temperature $${ 25 }^{ o }C$$ and the reaction is completed to give:
$${ Fe }_{ 2 }{ O }_{ 3 }(s)+2Al(s)\longrightarrow { Al }_{ 2 }{ O }_{ 3 }(s)+2Fe(l);\Delta H=-850kJ$$
The liberated heat is retained within the products, whose combined specific heat over a wide temperature range is about $$0.8J{ g }^{ -1 }{ K }^{ -1 }$$. The melting point of iron is $${ 1530 }^{ o }C$$. Show that the quantity of heat liberated is sufficient to raise the temperature of the product to the melting point of iron in order to get it welded.
A gas expands from a volume of $$3.0\ {dm}^{3}$$ to $$5.0\ {dm}^{3}$$ against a constant pressure of $$3.0$$ atm. The work done during expansion is used to heat $$10.0$$ mole of water of temperature $$290.0K$$. Calculate the final temperature of water (specific heat of water $$=4.184\ J\ { K }^{ -1 } { g }^{ -1 }$$)
A gas contained in a cylinder is filled with a frictionless piston expands against a constant pressure $$1$$ atmosphere from a volume of $$4$$ litre to a volume of $$14$$ litre. In doing so, it absorbs $$800J$$ thermal energy from surroundings. Determine $$\Delta U$$ for the process.
$$5$$ mole of oxygen are heated at constant volume from $${10}^{o}C$$ to $${20}^{o}C$$. What will be the change in the internal energy of gas? The molar heat of oxygen at constant pressure, $${C}_{P}=7.03cal$$ $${ mol }^{ -1 }{ deg }^{ -1 }$$ and $$R=8.31J\quad { mol }^{ -1 }{ deg }^{ -1 }$$.
Determine the heat of transformation of
$${C}_{(diamond)}\rightarrow {C}_{(graphite)}$$ from the following data
$${C}_{(diamond)}+{O}_{2}(g)\rightarrow C{CO}_{2}(g);(\Delta H=-94.5kcal)$$
$$ {C}_{(graphite)}+{O}_{2}(g)\rightarrow C{CO}_{2}(g);(\Delta H=-94.0kcal)$$
The equilibrium constant at $${25}^{o}C$$ for the process:
$${ Co }^{ 3+ }(aq.)+6{ NH }_{ 3 }(aq.)\rightleftharpoons { \left[ Co{ \left( { NH }_{ 3 } \right) }_{ 6 } \right] }^{ 3+ }(aq.)\quad $$ is $$\quad 2\times { 10 }^{ 7 }$$
Calculate the value of $$\Delta { G }^{ o }$$ at $${25}^{o}C$$. $$\left( R=8.314J{ K }^{ -1 }{ mol }^{ -1 } \right) $$
For the equilibirium,
$$P{ Cl }_{ 5 }(g)\rightleftharpoons P{ Cl }_{ 3 }(g)+{ Cl }_{ 2 }(g)$$
$${ K }_{ c }=1.8\times { 10 }^{ -7 }$$
Calculate $$\Delta { G }^{ o }$$ for the reaction $$\left( R=8.314J{ K }^{ -1 }{ mol }^{ -1 } \right) $$
For the reaction
$$2NO(g)+{ O }_{ 2 }(g)\longrightarrow 2N{ O }_{ 2 }(g)$$
Calculate $$\Delta G$$ at $$700\ K$$ when enthalpy and entropy changes are $$-113\ kJ{ mol }^{ -1 }$$ and $$-145\ J{ K }^{ -1 }{ mol }^{ -1 }\quad $$ respectively.
Zinc reacts with dilute hydochloric acid to give hydrogen at $${17}^{o}C$$. The enthalpy of the reaction is $$-12.55kJ{mol}^{-1}$$ of zinc and entropy change equals $$5.0J{ K }^{ -1 }{ mol }^{ -1 }$$ for the reaction. Calculate the free energy change and predict whether the reaction is spontaneous or not.
In the reaction
$${ A }^{ + }+B\longrightarrow A+{ B }^{ + }$$,
there is no entropy change. If enthalpy change is $$22kJ$$ of $${A}^{+}$$, calculate $$\Delta G$$ for the reaction.
$$\Delta H$$ and $$\Delta S$$ for the system
$${ H }_{ 2 }O(l)\rightleftharpoons { H }_{ 2 }O(g)$$
at $$1$$ atmospheric pressure are $$40.63\ kJ{ mol }^{ -1 }$$ and $$108.8\ J{ K }^{ -1 }{ mol }^{ -1 }$$ respectively. Calculate the temperature at which the rates of forward and backward reactions will be the same. Predict the sign of free energy for this transformation above this temperature.
For the reaction
$$SO{ Cl }_{ 2 }+{ H }_{ 2 }O\longrightarrow S{ O }_{ 2 }+2HCl$$
the enthalpy of reaction is $$49.4kJ$$ and the entropy of reaction is $$336J{K}^{-1}$$. Calculate $$\Delta G$$ at $$300K$$ and predict the nature of the reaction.
$$\Delta H$$ and $$\Delta S$$ for the reaction,
$${ Ag }_{ 2 }O(s)\longrightarrow 2Ag(s)+\cfrac { 1 }{ 2 } { O }_{ 2 }(g)$$
are $$30.56kJ{ mol }^{ -1 }$$ and $$66.0J{ K }^{ -1 }{ mol }^{ -1 }$$ respectively. Calculate the temperature at which free energy change for the reaction will be zero. Predict whether the forward reaction will be forward above or below this temperature.
Calculate the temperature at which liquid water will be in equilibrium with water vapour.
$$\Delta { H }_{ vap }=40.73\ kJ{ mol }^{ -1 }$$ and $$\Delta { S }_{ vap }=0.109\ kJ{ mol }^{ -1 }{ K }^{ -1 }$$
For the reaction, $${ Ag }_{ 2 }O(s)\rightleftharpoons 2Ag(s)+\cfrac { 1 }{ 2 } { O }_{ 2 }(g)$$
$$\Delta H,\Delta S,\Delta T$$ are $$40.63\ kJ\ { mol }^{ -1 },1.808\ J{ K }^{ -1 }{ mol }^{ -1 }$$ and $$373.4\ K$$ respectively. Free energy change $$\Delta G$$ of the reaction will be:
For the reaction,
$$4C(graphite)+5{ H }_{ 2 }\longrightarrow n{ C }_{ 4 }{ H }_{ 10 };\Delta { H }^{ o }=-124.73kJ\quad { mol }^{ -1 }$$
$$4C(graphite)+5{ H }_{ 2 }\longrightarrow iso-{ C }_{ 4 }{ H }_{ 10 };\Delta { S }^{ o }=-365.8J{ K }^{ -1 }{ mol }^{ -1 }\quad $$
$$\Delta { H }^{ o }=-131.6kJ\quad { mol }^{ -1 }$$
$$\Delta { S }^{ o }=-381.079J{ K }^{ -1 }{ mol }^{ -1 }$$
Indicate whether normal butane can be spontaneously converted to iso-butane or not.
All the energy released from the reaction $$X\rightarrow Y, \triangle_{r}G^{\circ} = -193\ kJ\ mol^{-1}$$ is used for oxidising $$M^{+}$$ as $$M^{+}\rightarrow M^{3+} + 2e^{-}, E^{\circ} = -0.25\ V$$. Under standard conditions, the number of moles of $$M^{+}$$ oxidised when one mole of $$X$$ is converted to $$Y$$ is: $$(F = 96500\ C\ mole^{-1})$$
$$Zn(s) + 2AgCl(s) \rightleftharpoons ZnCl_{2} (0.555\ M) + 2Ag(s)$$
$$E_0 = 1.015\ volt \left (\dfrac {dE}{dT}\right )_{P} = -4.02\times 10^{-4} volt$$ per degree.
Find $$\triangle G, \triangle S$$.
Commercial sample of $$H_2O_2$$ is labeled as $$10\ Volume$$. Its % strength is nearly:
The following data is known about the melting of $$KCl$$:
$$\Delta H=7.25kJ\quad { mol }^{ -1 };\Delta S=+0.007KJ{ K }^{ -1 }{ mol }^{ -1 }$$
Calculate its melting point.
Show that the reaction,
$$CO(g)+\cfrac { 1 }{ 2 } { O }_{ 2 }(g)\longrightarrow C{ O }_{ 2 }(g)$$
at $$300\ K$$ is spontaneous and exothermic, when the standard entropy change is $$-0.094\ kJ\ { mol }^{ -1 } {K}^{-1}$$. The standard Gibbs free energies of formation for $${CO}_{2}$$ and $$CO$$ are $$-394.4$$ and $$-137\ kJ\ { mol }^{ -1 }$$ respectively.
For the reaction,
$$\quad { Ag }_{ 2 }O\rightleftharpoons 2Ag(s)+\cfrac { 1 }{ 2 } { O }_{ 2 }(g)$$
Calculate the temperature at which free energy change is zero. At a temperature lower than this, predict whether the forward of the reverse reaction will be forward. Give reason
($$\Delta H=+30.56kJ;\Delta S==+0.066kJ{ K }^{ -1 }{ mol }^{ -1 }$$)
Show that the internal energy of the air (treated as an ideal gas) contained in a room remains constant as the temperature changes between day and night. Assume that the atmospheric around remains constant and the air in the room maintains this pressure by communicating with the surrounding through the windows etc.
Calculate the standard internal energy change for the reaction
$${C}_{(graphite)} + {H}_{2}O(g) \rightarrow CO(g) + {H}_{2}O(g)$$
$${\Delta} ^ {o}_{f}$$ at $$25^o$$; $${H}_{2}O(g) = -241.8 kJ {mol}^{-1}$$
$$CO(g) = -110.5 kJ {mol}^{-1}$$
$$R = 8.314 J{K}^{-1}{mol}^{-1}$$
The Born-Haber cycle for formation of rubidium chloride ($$RbCl$$)is given below (the enthalpies are in $$kCal$$ $${mol}^{-1}$$).
Find the value of $$X$$.
Heat of formotion = Heat of sublimation + Dessolution energy +Ionzation + energy + (electron affnutr+)
Substituting values
$$\Delta H_f =\Delta H_S +\Delta H_D +\Delta IE +\Delta E_a +\Delta U$$
$$-105=+20.5+28.75+96.0+X-159.5$$
$$\boxed {X=-90.75} \ Kcel /mol$$
Determine whether the following reaction will be spontaneous or nonspontaneous under standard conditions.
$$Zn(s) + Cu^{2+} (aq) \rightarrow Zn^{2+} (aq) + Cu (s) ,\ \ \ \Delta H^0 = -219 kJ, \\ \ \Delta S^0 = -21 JK^{-1}$$.
Calculate the heat change during the reaction $$24$$g C and $$128$$g S following :the change $$C+S_2\rightarrow CS_2$$; $$\Delta$$H$$=22$$K cal.
For a chemical reaction, $$\Delta H$$ and $$\Delta S$$ are negative. State, giving reason, under what conditions this reaction is expected to occur spontaneously.
For the reaction, $$2A(g)+B(g)\longrightarrow 2D(g),\Delta { U }=-10.5KJ$$ and $$ \Delta { S }=-44.10J{ K }^{ -1 }$$. Calculate $$ \Delta { G }$$ for the reaction and reaction and predict whether the reaction may occur spontaneously.
For a reaction both enthalpy change and entropy change are positive. Under what conditions the reaction will be spontaneous?
For the reaction:
$$2A(g)+B(g)\rightarrow 2D(g)$$,
$$\Delta U^{\ominus}=-10.5$$ kJ and $$\Delta S^{\ominus}=-44.1$$ $$JK^{-1}$$.Does the reaction occur spontaneously?
[Give your answer in terms of Yes or No]
$$\Delta U^{\ominus}=-10.5$$ kJ and $$\Delta S^{\ominus}=-44.1$$ $$JK^{-1}$$.Does the reaction occur spontaneously?
How do you define specific heat ? What is specific heat of water ?
Explain Third law of thermodynamics.
For oxidation of iron,
$$4Fe\left( s \right) +{ 3O }_{ 2 }\left( g \right) \rightarrow 2{ Fe }_{ 2 }{ O }_{ 3 }\left( s \right) $$entropy change is - 549.4 $${ JK }^{ -1 }{ mol }^{ -1 }$$ at 298 K. In spite of negative entropy change of this reaction, why is the reaction spontaneous?($$\triangle ,{ H }^{ \circleddash }$$ for this reaction is $$-1648\times { 10 }^{ 3 }J\quad { mol }^{ -1 }$$)
Many of the photochemical changes have positive sign of $$\delta G$$, yet they are spontaneous. Why?
What is specific heat?
If $$1.0 kcal$$ of heat is added to $$1.2 L$$ of $${ O }_{ 2 }$$ in a cylinder at constant pressure of $$1$$ atm, the volume increase to $$1.5 L$$. Calculate $$\Delta U$$ and $$\Delta H$$ of the process $$(1 L-atm=100 J)$$
Identify the correct statement regarding a spontaneous process
1) For a spontaneous process in an isolated system, the change in entropy is positive
2) Endothermic process are never spontaneous
3) Exothermic processes are always spontaneous (4) Lowering of energy in the reaction process is the only criterion for spontaneity
State and explain Hess's law of constant heat summation? Give its application.
Derive relationship between H and U.
Write the importance of Hess's law of constant heat summation.
A gas cylinder contains 14.2 Kg butane gas. it is consumption of energy in a family is 10000 KJ for cooking purposes how long this cylinder will be sufficient to supply. If the enthalpy of combustion of butane is 2658 KJ mol
How it is possible to find the value of $$\Delta U$$ and not the value of $$U$$
Calculate $$ \text E_{cell}$$ and $$ \Delta G $$ for the following $$28 ^ { \circ } \mathrm { C } :\mathrm { Mg } _ { ( s ) } + \mathrm { Sn } ^ { 2 + } ( 0.04 \mathrm { M } ) \rightarrow \mathrm { Mg } ^ { 2 + } ( 0.06 \mathrm { M } ) + \mathrm { Sn } _ { ( s ) }$$
$$ E _ { \text { cell } } ^ { \circ } = 2.23 \mathrm { V } $$
Is the reaction spontaneous?
The reaction of nitrogen with hydrogen to make ammonia has $$\Delta H=-92 kJ$$ $$N_2(g)+3H_2(g)\rightarrow2NH_3(g)$$. What is the value of $$\Delta U$$ (in kJ) if the reaction is carried out at a constant pressure of $$40\ bar$$ and the volume change is $$-1.25\ litre$$?
$$1g$$ of graphite is burnt in a bomb calorimeter in excess of oxygen at $$298\ K$$ and $$1$$ atmospheric pressure according to the equation.
$$C (graphite) + O_{2}(g) \rightarrow CO_{2}(g)$$
During the reaction, temperature rises from $$298 k$$ to $$299 k$$. If the heat capacity of the bomb calorimeter is $$20.7 kJ/K$$. What is the enthalpy change for the above reaction at $$298 K$$ and $$1 atm$$?
Calculate the $$\Delta_{r}H^{o}$$ at $$298\ K$$ for the reaction:
$$C(graphite)+2H_{2}(g)\rightarrow CH_{4}(g)$$
from the following date:
$$C(graphite)+O_{2}(g)\rightarrow CO_{2}(g)
\\ \Delta_{r}H^{o}=-393.5\ kJ\ mol^{-1} \\
H_{2}(g)+\dfrac {1}{2}O_{2}(g)\rightarrow H_{2}O(l)\\ \Delta_{r}H^{o}=-285.8\ kJ\ mol^{-1}$$
$$CO_{2}(g)+2H_{2}O(l)\rightarrow CH_{4}(g)+2O{2}(g)\\
\Delta_{r}H^{o}=+890.3\ kJ\ mol^{-1}$$
Water can be lifted into the water tank at the top of the house with the help of a pump. Then why is it not considered to be spontaneous?
A chemical reaction is spontaneous at 298K and non-spontaneous at 350K. Which of the following is correct for the reaction?
| s.no | $$\Delta G$$ | $$\Delta H$$ | $$\Delta S$$ |
| A) | - | - | + |
| B) | + | + | + |
| C) | - | + | - |
| D) | + | - | + |
| E) | - | - | - |
When a substance having mass 3 kg receives 600 cal of heat, its temperature increases by $$10^0$$C. What is the specific heat of the substance?
Calculate $$\triangle G$$ for the reaction at 298 K$$2SO_2(g)+O_2(g)\longrightarrow 2SO_3(g)$$, $$\triangle { G }^{ o }=-142 kJ{ mol }^{ -1 }$$
If partial pressures of $$SO_2$$, $$O_2$$ and $$SO_3$$ are 50 atm 75 atm and 2 atm respectively at $$298 K$$
If partial pressures of $$SO_2$$, $$O_2$$ and $$SO_3$$ are 50 atm 75 atm and 2 atm respectively at $$298 K$$
Explain why:
Ice at zero degrees centigrade has a greater cooling effect than water at $$0 ^\circ C$$.
What is the need to heat solution ?
At $$298 \mathrm{K}$$. $$\mathrm{K}_{\mathrm{p}}$$
for the reaction $$N_{2} O_{4}(g) \rightleftarrows 2 \mathrm{NO}_{2}(g)$$ is
0.98 . Predict whether the reaction is spontaneous or not.
Given that $$\Delta
H=0$$ for mixing of two gases. Explain whether the diffusion of these gases
into each other in a closed container is a spontaneous process or not?
Explain the meaning of thermochemical equation for the reaction:
$$2H_{2}(g)+O_{2}(g)\rightarrow 2H_{2}O(l)+136kcal$$.
What is spontaneous process? Give example.
Justify the following statements:
(a) An exothermic reaction is always thermodynamically spontaneous.
(b) The entropy of a substance increases on going from liquid to vapour state at any temperature.
Evaporation of water is an endothermic process but spontaneous. Explain.
What is meant by entropy driven reaction? How can a reaction with positive changes of enthalpy and entropy be made entropy driven?
Define non-spontaneous process.
What are the applications of Hess's law of constant heat summation?
What is meant by the free energy of a system? What will be the direction of chemical reaction when
(i) $$\Delta G=0$$
(ii) $$\Delta G>0$$
(iii) $$\Delta G<0$$
Give Hess's Law of constant Heat summetion and write its uses.
This law is given by a russian chemist G.H. Hess , in $$ 1840 $$ the law is known after his name as Hess's law . it states thatl:
"If a reaction takes place in several steps then its standard reaction entahlpy is the sum of the standard enthalpies of the intermediate reactions into which the overall reaction may be divide at the same temperature".
In general if the enthalpy of an overall reaction $$ A \rightarrow B $$ along one route is $$ \Delta H $$ and $$ H_1, H_2, H_3 .......$$
Representing enthalpies of reactions leading to same product B along another route , if the reaction is taking place in three steps, then we have
$$ \Delta H = H_1 +H_2 + H_3 $$
It can be represented as :
example : Combustion of carbon dioxide can be done in two ways :
$$ Path I : C_{(s)} + O_{ 2(g)} CO_{ 2(g) } \Delta H = - 393.5 kJ $$
$$ Path II : C_{(s)} + \frac {1}{2} O_{2(g)} \Delta H_1 = -110.5 kJ $$
$$ CO_{(g)} + \frac {1}{2}O_{2(g)} \rightarrow CO_{2(g)} \Delta H_2 = -283.0 kJ $$
In both the cases,
$$ \Delta H_1 +\Delta H_2 = ....393.5kJ $$
Thus the heat of reaction in single step and that in two steps is same. this proves Hess's law .
uses of Hess's law of constant heat :
1. Determination of transition : it helps in the determination of entahlpy of transition during allotropic modification.
2. Determination of enthalpy of formation : it helps in the determination of enthalpy of formation which cannot be determined experimentally e.g it is not possible to calculate enthalpy of formation of CO experimentally but can be calculated by hess's law.
Bond energy : It may be defined as "the quantity of heat evolved when a bond is formed between two free atoms in a gaseous state to form a molecular product in a gaseous state".It is also known as enthalpy of formation of the bond . it mat also be defined as "the average quantity of heat required to break (dissociate) bonds of that type present in one mole of the compound."
"If a reaction takes place in several steps then its standard reaction entahlpy is the sum of the standard enthalpies of the intermediate reactions into which the overall reaction may be divide at the same temperature".
In general if the enthalpy of an overall reaction $$ A \rightarrow B $$ along one route is $$ \Delta H $$ and $$ H_1, H_2, H_3 .......$$
Representing enthalpies of reactions leading to same product B along another route , if the reaction is taking place in three steps, then we have
$$ \Delta H = H_1 +H_2 + H_3 $$
It can be represented as :
example : Combustion of carbon dioxide can be done in two ways :
$$ Path I : C_{(s)} + O_{ 2(g)} CO_{ 2(g) } \Delta H = - 393.5 kJ $$
$$ Path II : C_{(s)} + \frac {1}{2} O_{2(g)} \Delta H_1 = -110.5 kJ $$
$$ CO_{(g)} + \frac {1}{2}O_{2(g)} \rightarrow CO_{2(g)} \Delta H_2 = -283.0 kJ $$
In both the cases,
$$ \Delta H_1 +\Delta H_2 = ....393.5kJ $$
Thus the heat of reaction in single step and that in two steps is same. this proves Hess's law .
uses of Hess's law of constant heat :
1. Determination of transition : it helps in the determination of entahlpy of transition during allotropic modification.
2. Determination of enthalpy of formation : it helps in the determination of enthalpy of formation which cannot be determined experimentally e.g it is not possible to calculate enthalpy of formation of CO experimentally but can be calculated by hess's law.
Bond energy : It may be defined as "the quantity of heat evolved when a bond is formed between two free atoms in a gaseous state to form a molecular product in a gaseous state".It is also known as enthalpy of formation of the bond . it mat also be defined as "the average quantity of heat required to break (dissociate) bonds of that type present in one mole of the compound."
What will be the sign of $$ G $$ for melting of ice at $$ 267 K $$ and $$ 276 K $$? (Melting point of ice=$$ 272 K $$).
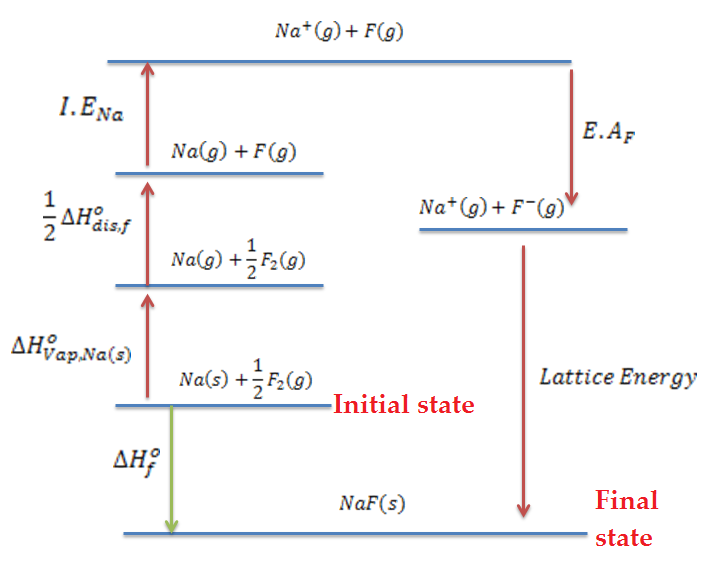
Explain the steps involved in Born Haber cycle for the formation of NaCl.
Why most of the exothermic processes (reactions) are spontaneous?
In a constant volume calorimeter, $$3.5$$ g of a gas with molecular weight $$28$$ was burnt in excess oxygen at $$298.0$$ K. The temperature of the calorimeter was found to increase from $$298.0$$ K to $$298.45$$ K due to the combustion process. Given that the heat capacity of the calorimeter is $$2.5$$ kJ K$$^{-1}$$, the numerical value for the enthalpy of combustion of the gas in kJmol$$^{-1}$$ is:
$$200$$ ml of $$1$$M $$HCl$$ is mixed with $$400$$ ml of $$0.5$$M $$NaOH$$. The temperature rise in the calorimeter was found to be $$4.0^{o}C.$$ Water equivalent of calorimeter is $$25$$g and the specific heat of the solution is $$1$$ cal/mL/degree. If the theoritical heat of neutralization of a strong acid and strong base is $$-13.5$$ kcal, then the percentage error (as nearest integer) incurred in this experiment while calculating the heat of neutralization is
It is observed that the functioning of neuronal circuits in our brain is driven by the energy available from the combustion of glucose. Calculate the amount of glucose (in gm) which should be burnt per hour to produce sufficient energy for the brain, which operates at $$\dfrac{128}{9}$$ watts.
Given : $$|\Delta H^{0}|$$ of combustion of glucose at 400 K = $$3000$$ kJ/mol
$$|\Delta S^{0}|$$ of combustion of glucose at 400 K= $$180$$ J/mol K
$$|\Delta S^{0}|$$ of combustion of glucose at 400 K= $$180$$ J/mol K
From the following data at $$\displaystyle 25^{\circ}C$$, The standard enthalpy of formation of FeO(s) is X, then 0.3-X is:
Reaction $$\displaystyle \Delta _{r}H^{\circ}$$ ( kJ / mole ) $$\displaystyle Fe_{2}O_{3}(s)+3C (graphite)\rightarrow 2Fe(s)+3CO(g)$$ 492.6 $$\displaystyle FeO(s)+C (graphite)\rightarrow Fe(s)+CO(g)$$ 155.8 $$\displaystyle C (graphite)+O_{2}(g)\rightarrow CO_{2}(g)$$ $$\displaystyle -$$393.51 $$\displaystyle CO(g)+1/2\: O_{2}(g)\rightarrow CO_{2}(g)$$ $$\displaystyle -$$282.98
| Reaction | $$\displaystyle \Delta _{r}H^{\circ}$$ ( kJ / mole ) |
| $$\displaystyle Fe_{2}O_{3}(s)+3C (graphite)\rightarrow 2Fe(s)+3CO(g)$$ | 492.6 |
| $$\displaystyle FeO(s)+C (graphite)\rightarrow Fe(s)+CO(g)$$ | 155.8 |
| $$\displaystyle C (graphite)+O_{2}(g)\rightarrow CO_{2}(g)$$ | $$\displaystyle -$$393.51 |
| $$\displaystyle CO(g)+1/2\: O_{2}(g)\rightarrow CO_{2}(g)$$ | $$\displaystyle -$$282.98 |
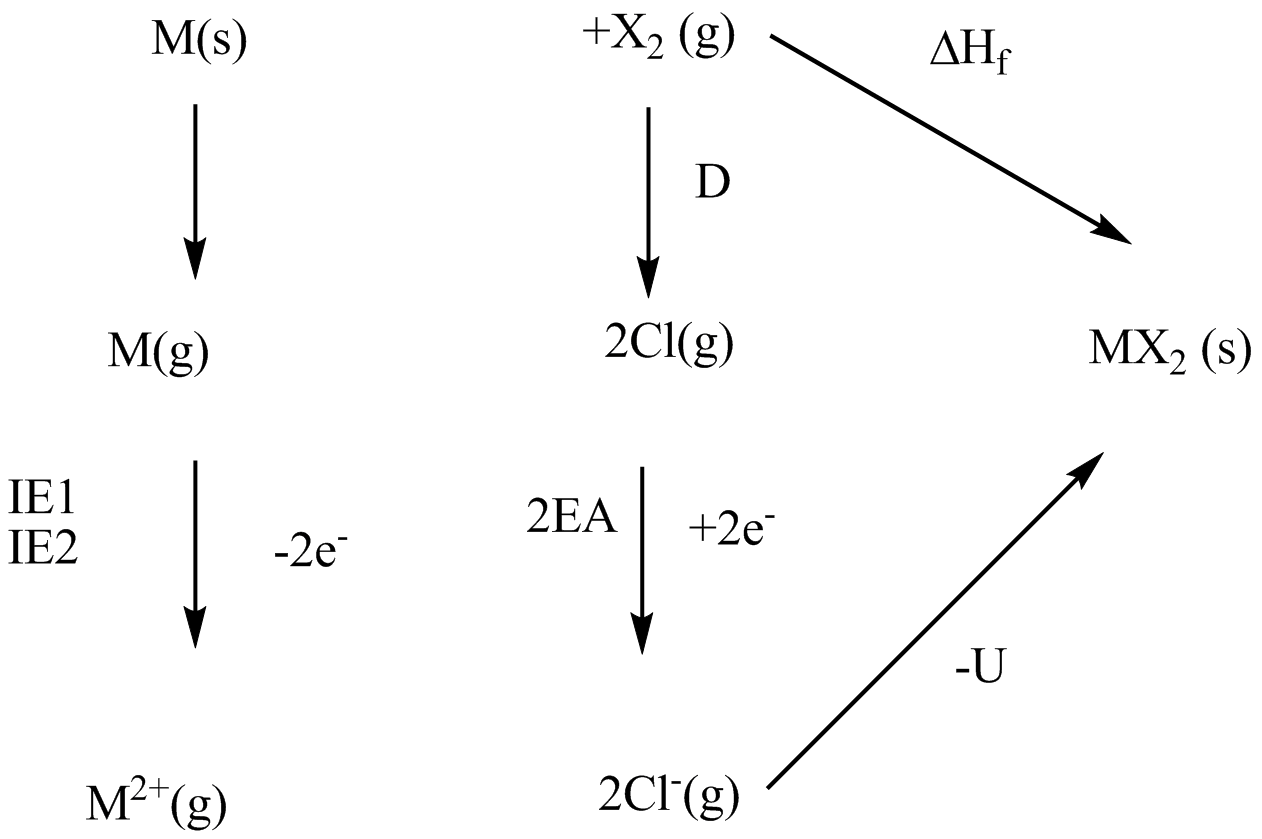
For the ionic solid $$MX_{2}$$,where X is monovalent ,the enthalpsy of formation of the solid from M(s) and $$X_{2}$$(g) is 1.5 times the electron gain enthalpsy of X(g).the first and second ionisation enthalpsy of the metal(M) are 1.2 and 2.8 times of the enthalpsy of sublimation of M(s).the bond dissociation enthalpy of $$X_{2}$$(g) is 0.8 times the first ionisation enthaply of metal and it is also equal to one-fifth of the magnitude of lattice enthalpy of $$MX_{2}$$. If the electron gain enthalpy of X(g) is $$96$$Kcal/mol, find the enthalpy of sublimation of metal(M) in Kcal/mol.(Round off answer to integer).
$$\Delta H_f =S +D+IE_1 + IE_2 + 2EA +U$$
Substitute values in the above expression.
$$1.5 \times (-96 ) = S+0.8 IE_1+IE_1+IE_2+2(-96) +5IE_1$$
$$1.5 \times (-96) = S + 6.8 (1.2S) + 2.85 +2(-96)$$
Hence, $$S=41.38 \ kcal/mol$$.
If X is the lattice entahlpy of $$Ca{Cl}_{2}$$ ,find $$X$$. Given that the enthalpy of
(i) sublimation of $$Ca$$ is $$121kJ{ mol }^{ -1 }$$
(ii) dissociation of $${Cl}_{2}$$ to $$Cl$$ is $$242.8kJ{ mol }^{ -1 }$$;
(iii) ionization of $$Ca$$ to $${Ca}^{2+}$$ is $$2422kJ{ mol }^{ -1 }$$;
(iv) electron gain enthalpy for $$Cl$$ to $${Cl}^{-}$$ is $$-355kJ{ mol }^{ -1 }$$;
(iv) $${ \Delta }_{ f }H$$ overall is $$-795kJ{ mol }^{ -1 }$$.
Calculate the lattice enthalpy(nearest integer value) in $$kJ{ mol }^{ -1 }$$ of $$LiF$$, given that enthalpy of,
(i) sublimation of lithium is $$155.3kJ$$ $${ mol }^{ -1 }$$;
(ii) dissociation of $$1/2$$ mole of $${F}_{2}$$ is $$75.3kJ$$;
(iii) ionization enthalpy of lithium is $$520kJ$$ $${ mol }^{ -1 }$$;
(iv) electron gain enthalpy of 1 mole of $$F(g)$$ is $$-333kJ$$;
(v) $${ \Delta }_{ f }H$$ overall is $$-594kJ$$ $${ mol }^{ -1 }$$.
The standard enthalpy of formation of $$FeO$$ and $$Fe_2O_3$$ is $$-65 \: kcal \: mol^{-1}$$ and $$-197 \: kcal \: mol^{-1}$$ respectively. If a mixture containing $$FeO$$ and $$FeO_3$$ in $$2 : 1$$ mole ratio on oxidation is changed into $$1 : 2$$ mole ratio, thermal energy in kcal released per $$6$$ mole of mixture will be (nearest integer)____________.
The endothermic reaction of carbon (graphite) in super heated steam at 500 K $$[i.e., C_{graphite} +H_2O(g)\longrightarrow CO(g)+ H_2 (g)]$$
is made by providing heat by burning a part of carbon (graphite) in $$O_2(g)$$ followed by an exothermic reaction :$$[C_{graphite} +O_2(g)\longrightarrow CO_2(g);\:\Delta H= -393.7 \: kJ \: mol^{-1} \: at \: 500K]$$.
If a total of 1.34 mole of graphite is required for the production of 1 mole of $$H_2$$ at 500 K, the heat of reaction for carbon (graphite) with $$H_2O$$ in kJ is ________.
6.80 g of $$NH_3$$; is passed over heated CuO. The standard heat enthalpIes of $$NH_{3}$$, $$CuO(s)$$ and $$H_20(l)$$ are -46.0, -155.0 and $$-285 0 \: kJ \: mol^{-1}$$ respectively and the change is.
$$NH_3 +(3/2)CuO\longrightarrow \frac{1}{2}N_2(g)+ (3/2)H_2O(l) +(3/2)Cu(s)$$.
If the enthalpy change is $$x$$ kJ then $$-\dfrac{x}{15}$$ (nearest integer) is___________.
The dissolution of 1 mole of NaOH(s) in $$100$$ mole of $$H_2O(l)$$ give rise to evolution of heat as -42.34 kJ. However, if 1 mole of NaOH(s) is dissolved in $$1000$$ mole of $$H_2O(l)$$ the heat given out is 42.76 kJ. If the enthalpy change when $$900$$ mole of $$H_2O(l) $$ are added to a solution containing 1 mole of NaOH(s) in $$100 $$ mole of $$H_2O$$ is $$x$$ $$kJ$$ then the value of $$-100x$$ is _____.
Calculate the resonance energy of $$C_6H_6$$, using Kekule formula for $$C_6H_6$$ from the following data: (i) $$\Delta H^{\circ}$$ for $$C_6H_6 = -358.5 \: kJ \: mol^{-1}$$ (ii) $$Heat \: of \: atomisation \: of \: C = 716.8\: kJ \: mol^{-1}$$ (iii) Bond energy of $$C-\! \! \! -H, \;C-\! \! \! -C, \:C=\! \! =C$$ and $$H-\! \! \! -H$$ are 490, 340, 620 and $$436.9 \: kJ \: mol^{-1}$$. Report your answer in kj (only value).
$$2C_4H_{10}\longrightarrow C_8H_{18}+H_2$$. Given that bond energy of $$C -C,\:C -H$$ are $$347.3$$ and $$414.2$$ kJ mol$$^{-1}$$ and the heat of formation of hydrogen atom is $$217.55$$ kJ mol$$^{-1}$$. Find $$\Delta H $$ for the above reaction in kJ mol$$^{-1}$$.(If $$\Delta H=x$$, input the answer to the nearest integer as $$\dfrac{x}{9}$$).
The heat of combustion of acetylene is 312 kcal. If heat of formation of $$CO_2$$ and $$H_2O$$ are 94.38 and 68.38 kcal respectively, $$C \equiv\!\! \equiv C \:$$ bond energy is $$x \:kcal $$. Given that heat of atomisation of C and H are 150.0 and 51.5 kcal respectively and $$C-\! \! \! -H$$ bond energy is 93.64 kcal.
Value of $$x$$ (nearest integer value) is _______.
Value of $$x$$ (nearest integer value) is _______.
Exactly 3.0 g of carbon was burned to $$\displaystyle { CO }_{ 2 }$$ in copper calorimeter. The mass of calorimeter is 1.5kg and the mass of water in calorimeter is 2kg. The initial temperature was $$\displaystyle { 20 }^{ o }C$$ and the final temperature was $$\displaystyle { 31.3 }^{ o }C$$. If specific heat of copper is $$\displaystyle 0.0826\,cal/g-K$$, the heat value to closest integer of carbon in kcal/g is
A new element $$E$$ forms a compound with chlorine which contains 1.455 g $$\displaystyle Cl$$ per $$\displaystyle g\ E$$. The specific heat of $$E$$ was found $$0.05\ cal/g$$ . If eq. weight of element is 24, then the value of $$\displaystyle x$$ in $$\displaystyle { ECl }_{ x }$$ is:
The enthalpy changes of some process are given below :
$$\alpha\! -\! D\! -\! glucose_{(s)}+ H_2O\longrightarrow \alpha\! -\! D\! -\! glucose_{(aq)}; \quad \Delta H_{dissolution}= 10.84 \:kJ$$.
$$\beta \! -\! D\! -\! glucose_{(s)}+ H_2O\longrightarrow \beta \! -\! D\! -\! glucose_{(aq)}; \quad \Delta H_{ dissolution}= 4.68 \:kJ$$.
$$\alpha\! -\! D\! -\! glucose_{(aq)}\longrightarrow \beta \! -\! D\! -\! glucose_{(aq)}; \: \quad \Delta H_{mutarotation} = -1.16 \:kJ$$
The $$\Delta H^{\circ}$$ for $$\alpha\! -\! D\! -\! glucose\longrightarrow \beta \! -\! D\! -\! glucose$$ is :
$$\beta \! -\! D\! -\! glucose_{(s)}+ H_2O\longrightarrow \beta \! -\! D\! -\! glucose_{(aq)}; \quad \Delta H_{ dissolution}= 4.68 \:kJ$$.
$$\alpha\! -\! D\! -\! glucose_{(aq)}\longrightarrow \beta \! -\! D\! -\! glucose_{(aq)}; \: \quad \Delta H_{mutarotation} = -1.16 \:kJ$$
The $$\Delta H^{\circ}$$ for $$\alpha\! -\! D\! -\! glucose\longrightarrow \beta \! -\! D\! -\! glucose$$ is :
If $$\displaystyle \Delta G$$ and $$\displaystyle \Delta S$$ for the reaction: $$\displaystyle A(g)+B(g)\rightarrow P(g)$$, at 300 K are $$\displaystyle -600$$ cal and $$\displaystyle -10\;cal/K$$. Then $$\displaystyle \Delta H$$ for the reaction in kcal is ______.
$$\Delta H^{\circ}_f$$ of $$Fe_2O_3$$ and $$Al_2O_3$$ are -189 kJ and -405 kJ respectively. How much heat (in kJ) is given out during reaction of 1 g Al according to
$$2Al +Fe_2O_3\longrightarrow Al_2O_3 +2Fe$$ ?
$$KCl_{(s)} \longrightarrow K^ + + Cl^-$$
The heat evolved in kcal for the process at $$250^{\circ}C$$ of dissolving 1.0 mole of KCl in excess of water is __________. [Given: $$\Delta H^{\circ}_f$$ of $$K^+_{(aq)}, \:Cl^-_{(aq)}$$ and $$KCl_{(s)}$$ are -60, -40 and -104 kcal/mole]
[Given: $$\Delta H^{\circ}_f$$ of $$K^+_{(aq)}, \:Cl^-_{(aq)}$$ and $$KCl_{(s)}$$ are -60, -40 and -104 kcal/mole]
If heat of formation of $$CaCl_2$$ and $$NaCl$$ are 191 and 97.5 kcal, the heat of reaction for $$CaCl_2 + 2Na \longrightarrow 2NaCl + Ca$$ is:
Match the Following:
The matched pairs are shown below.
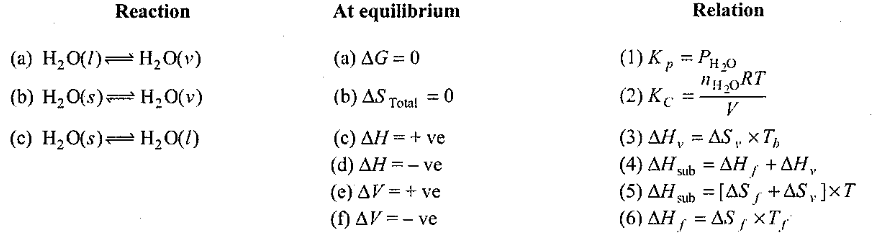
The enthalpies of neutralisation of $$NaOH$$ and $${NH}_{4}OH$$ by $$HCl$$ are $$-13680$$ calories and $$-12270cal$$ respectively. What would be the enthalpy change of one gram equivalent of $$NaOH$$ is added to one gram equivalent of $${NH}_{4}Cl$$ is solution? Assume that $${NH}_{4}OH$$ and $$NaCl$$ are quantitatively obtained (only magnitude in cal).
The standard heats of formation of $${CH}_{4}(g), {CO}_{2}(g)$$ and $${H}_{2}O(l)$$ are $$-76.2, -398.8, -241.6kJ{mol}^{-1}$$. Calculate amount of heat evolved by burning $$1\ {m}^{3}$$ of methane measured under normal (STP) conditions (nearest number in MJ).
Calculate the enthalpy change when infinitely dilute solution of $$Ca{Cl}_{2}$$ and $${Na}_{2}{CO}_{3}$$ mixed $$\Delta {H}^{o}_{r}$$ for $${Ca}^{2+}(aq)$$, $${CO}_{3}^{2-}(aq)$$ and $$Ca{CO}_{3}(s)$$ are $$-129.80, -161.65, -288.5 kcal$$ $${mol}^{-1}$$ respectively (nearest number in kcal).
Calculate the electron affinity of fluorine atom using the following data (only magnitude in nearest integer in kj/mol). All the values are in $$kJ$$ $${mol}^{-1}$$ at $${25}^{o}C$$, $$\Delta{H}_{diss}({F}_{2})=160$$; $$\Delta {H}^{o}_{r}$$ ($$NaF(s))=-571;\ I.E$$ $$[Na(g)]=494, \ \Delta {H}_{vap}[Na(s)]=101$$. Lattice energy of $$NaF(s)=-894$$.
From Born-Hyber cycle in the diagram,
$$\Delta H^o_f = \Delta H^o_{vap,\; Na(s)} +\frac{1}{2}\Delta H^o_{dis,\; F}+I.E_{Na}+E.A_{F}+L.E_{NaF}$$
On simplifying
$$E.A_{F} = \Delta H^o_f -\Delta H^o_{vap,\; Na(s)} -\frac{1}{2}\Delta H^o_{dis,\; F}-I.E_{Na}-L.E_{NaF}$$
$$\Rightarrow E.A_{F}=-571-101-\frac{1}{2}\times 160-494+894= -352 \; kJ/mol$$
List equation/law (in Column I) with statement (in Column II).Match the following.
Becker and Ruth measured the heat evolved in the following processes at $${20}^{o}C$$: (1) $$1$$ mole of solid $${({COONH}_{4})}_{2}{H}_{2}O$$ is burned in oxygen, (2) $$1$$ mole of solid $${(COOH)}_{2}{({H}_{2}O)}_{2}$$ is burned in oxygen, (3) $$1$$ mole of solid $${({COONH}_{4})}_{2}{H}_{2}O$$ is dissolved in a large excess of water, (4) $$1$$ mole of solid $${(COOH)}_{2}{({H}_{2}O)}_{2}$$ is dissolved in a large excess of water, (5) $$1$$ mole of oxalic acid in dilute solution is neutralized with gaseous ammonia. They found (1) $$189.86kcal$$, (2) $$53.10kcal$$, (3) $$-11.47kcal$$, (4) $$-8.62kcal$$, (5) $$43.13kcal$$; (1) and (2) were measured at constant volume, the others at constant pressure. The end products of (1) and (2) were nitrogen, carbon-di-oxide and water. The heat of formation for $$1$$ mole of water from the elements had previously been determined as $$68.35kcal$$ at constant pressure and $${20}^{o}C$$. Find the change in enthalpy when $$1$$ mole of $${NH}_{3}$$ is formed from the elements at $${20}^{o}C$$ (only magnitude in nearest integer in kcal)
For the hypothetical reaction,
$$\displaystyle A_{2}g+B_{2}\left ( g \right )\rightleftharpoons 2AB\left ( g \right )$$
If $$\displaystyle \Delta _{r}G^{\circ}\: and\: \Delta _{r}S^{\circ}$$ are 20 kj/mol and -20 $$\displaystyle JK^{-1}mol^{-1}$$ respectively at 200 K
$$\displaystyle \Delta _{r}C_{P}\: is\: 20JK^{-1}mol^{-1}$$ then value $$\displaystyle \frac{\Delta _{r}H^{\circ}}{10}$$ of (KJ/mol) at 400 K is:
For the hypothetical reaction, $$\displaystyle { A }_{ 2 }\left( g \right) +{ B }_{ 2 }\left( g \right) \rightleftharpoons 2AB\left( g \right) $$, if $$\displaystyle { \Delta }_{ r }{ G }^{ o }$$ and $$\displaystyle { \Delta }_{ r }{ S }^{ o }$$ are $$\displaystyle 20\ { kJ }/{ mol }$$ and $$\displaystyle -20 \ { JK }^{ -1 }{ mol }^{ -1 }$$ respectively at 200 K. $$\Delta _rC_p$$ is $$20\ JK^{-1}mol^{-1}$$.
Then value $$\displaystyle \frac { { \Delta }_{ r }{ H }^{ o } }{ 10 } $$ of ($$kJ/mol$$) at 400 K is:
For the reaction at 298 K, 2A+B $$ \displaystyle \rightarrow C $$
$$ \displaystyle \bigtriangleup $$ H = 400 KJ $$ \displaystyle mol^{-1} $$ and $$ \displaystyle \bigtriangleup $$ S = 0.02 KJ $$ \displaystyle K^{-1} $$ $$ \displaystyle mol^{-1} $$
At what temperature will the reaction become spontaneous considering $$ \displaystyle \bigtriangleup $$ H and $$ \displaystyle \bigtriangleup $$ S to be constant over the temperature range?
$$ \displaystyle \bigtriangleup $$ H = 400 KJ $$ \displaystyle mol^{-1} $$ and $$ \displaystyle \bigtriangleup $$ S = 0.02 KJ $$ \displaystyle K^{-1} $$ $$ \displaystyle mol^{-1} $$
At what temperature will the reaction become spontaneous considering $$ \displaystyle \bigtriangleup $$ H and $$ \displaystyle \bigtriangleup $$ S to be constant over the temperature range?
The equilibrium constant for a reaction iswhat will be value of $$ \displaystyle \bigtriangleup G^{\ominus } $$ ? R =8.314 $$ \displaystyle JK^{-1} mol^{-1} $$, T=300 K
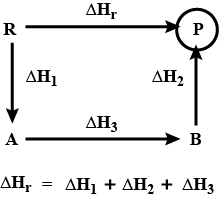
Calculate the value of $${ \Delta H }/{ kJ }$$ for the following reaction using the listed thermochemical equations:
$$2C\left( s \right) +{ H }_{ 2 }\left( g \right) \longrightarrow { C }_{ 2 }{ H }_{ 2 }\left( g \right) $$
$$2{ C }_{ 2 }{ H }_{ 2 }\left( g \right) +5{ O }_{ 2 }\left( g \right) \longrightarrow 4C{ O }_{ 2 }\left( g \right) +2{ H }_{ 2 }O\left( I \right) { \Delta H }/{ kJ }=-2600kJ$$
$$C\left( s \right) +{ O }_{ 2 }\left( g \right) \longrightarrow C{ O }_{ 2 }\left( g \right) { \Delta H }/{ kJ }=-390kJ$$
$$2{ H }_{ 2 }\left( g \right) +{ O }_{ 2 }\left( g \right) \longrightarrow 2{ H }_{ 2 }O\left( I \right) { \Delta H }/{ kJ }=-572kJ$$
Calculate $$E_{cell}$$ and $$\Delta$$G for the following at $$28^o$$C
$$Mg(s)+Sn^{2+}(0.025M)\rightarrow Mg^{2+}(0.06M)+Sn_{(s)}$$
$$E^0_{cell}=2.23$$V
Is the reaction spontaneous?
$$Mg(s)+Sn^{2+}(0.025M)\rightarrow Mg^{2+}(0.06M)+Sn_{(s)}$$
$$E^0_{cell}=2.23$$V
Is the reaction spontaneous?
Give the characteristics of free energy.
For a chemical reaction the values of $$\Delta H$$ and $$\Delta S$$ at 400 K are -10 K cal mol$$^{-1}$$ and 20 cal. deg$$^{-1}$$ mol$$^{-1}$$ respectively. Calculate the value of $$\Delta G$$ of the reaction.
Calculate $$q.w.\Delta U$$ and $$\Delta H$$ for the reversible isothermal expansion of one mole of an ideal gas at $${127}^{o}C$$ from a volume of $$10\ {dm}^{3}$$ to $$20\ {dm}^{3}$$.
Pressure over $$1000\ ml$$ of a liquid is gradually increases from $$1$$ bar to $$1001$$ bar under adiabatic conditions. If the final volume of the liquid is $$990\ ml$$, calculate $$\triangle U$$ and $$\triangle H$$ of the process, assuming linear variation of volume with pressure.
Explain spontaneous and non-spontaneous processes, giving two examples of each.
One mole of ethane was burnt in oxygen at constant volume to give $$C{O}_{2}$$ at 298 K. The heat evolved was found to be 1554 kJ. Calculate the heat of reaction at constant pressure.
Five moles of an ideal gas at $$300K$$, expanded isothermally from an initial pressure of $$4\ atm$$ to a final pressure of $$1\ atm$$ against a cont. ext. pressure of $$1\ atm$$. Calculate $$q, w, \triangle U$$ and $$\triangle H$$. Calculate the corresponding value of all if the above process is carried out reversibly.
The volume of a gas at STP is 2 L, 300 J heat is given to it, as a result of which volume changes to 2.5 L at 1 atm. Calculate the change in internal energy of the system.
What will be the final temperature attained if all the heat released in neutralization of $$1$$L of $$0.2$$M $$NH_4OH$$ with $$2$$L of $$0.1$$M HCl increases the temperature of the final solution having density $$0.95$$ gm/ml and specific heat capacity = $$13J/g^0C$$, if original temperature was $$27^0C$$? Assume weak base to be completely unionized.
The cell in which the following reaction occurs:
$$2{\text{F}}{{\text{e}}^{{\text{3 + }}}}\left( {{\text{aq}}} \right) + 2{{\text{I}}^{\text{ - }}}\left( {{\text{aq}}} \right) \to 2{\text{F}}{{\text{e}}^{{\text{2 + }}}}\left( {{\text{aq}}} \right) + {{\text{I}}_{\text{2}}}\left( {\text{s}} \right)\,{\text{has}}\,{\text{E}}_{\left( {{\text{cell}}} \right)}^ \odot = 0.236\,{\text{V}}$$ at 298 K.
Calculate the standard Gibbs energy and the equilibrium constant of the cell reaction.
Calculate the standard Gibbs energy and the equilibrium constant of the cell reaction.
$$\Delta { H }^{ 0 }\quad and \quad \Delta { S }^{ 0 }\quad for\quad CC{ l }_{ 4 }$$ are $$ 2.5{ KJ }^{ -1 }{ mol }^{ -1 }\quad $\quad 9.99{ JK }^{ -1 }{ mol }^{ -1 }$$ respectably at $$ 29{ 8 }^{ 0 }K$$ find the temperature at which solid $${ CCl }_{ 4 }$$ and its liquid are in equilibrium at one atmosphere.
$$100kJ$$ heat is transferred from a larger heat reservoir at $$400K$$ to another large heat reservoir at $$300K$$. Suppose there is no change in temperature due to exchange of heat:
Find (a) $$\Delta {S}_{source}$$, (b) $$\Delta{S}_{sink}$$ and (c) $$\Delta {S}_{total}$$. Comment on spontaneity of process:
Determine whether the following reaction will be spontaneous or non-spontaneous under standard conditions.$$Zn\left( s \right) +{ Cu }^{ 2+ }\left( a \right) \longrightarrow { Zn }^{ 2+ }\left( aq \right) +Cu\left( s \right) \triangle { H }^{ 0 }=-219kJ,\triangle { S }^{ 0 }=-21{ JK }^{ -1 }\left( Spontaneous \right) $$
A heat engine absorbs $$760kJ$$ heat from a source at $$380K$$. It rejects (i) $$650kJ$$, (ii) $$560kJ$$, (iii) $$504kJ$$ of heat to sink at $$280K$$. State which of these represent a reversible, an irreversible or an impossible cycle.
In the following reaction $$2{H_2}{O_2}\left( {aq} \right) \to 2{H_2}O\left( \ell \right) + {O_2}\left( g \right)$$ rate of formation of $${O_2}{\text{ is }}36g{\min ^{ - 1}},$$
(a) What is the rate of formation of $${H_2}O$$
(b) What is the rate of disappearance of $${H_2}O$$.
a) The enthalpy of combustion of methane, graphite and dihydrogen at 298 K are $$-890.3 kJ\quad { }^{ -1 }$$, $$-393.5 kJ\quad { }^{ -1 }$$ and $$-285.8 kJ\quad { }^{ -1 }$$ respectively. Calculate the enthalpy of formation of $${ CH }_{ 4 }\left( g \right) $$
b) Write the relationship between Gibb's energy, equilibrium constant and change in enthalpy.
For the reaction $$NH_4Cl(S) \rightarrow NH_3(g) + HCl(g)$$ at $$25^0$$C, enthalpy change $$\triangle = +177 kJ mol^{-1}$$ and entropy change $$\triangle S = +285 JK^{-1}mol^{-1}$$. Calculate free energy change $$\triangle G$$ at $$25^0$$C and product whether the reaction is spontaneous or not.
State and explain Hesss law of constant heat summation. What is the value of $$ \triangle { S }^{ o }_{ surr. }$$] for the following reaction at $$298\ K$$
$$ { 6CO }_{ 2\left( g \right) }+{ 6H }_{ 2 }{ O }_{ \left( 1 \right) }\rightarrow { C }_{ 6 }{ H }_{ 12 }{ O }_{ 6\left( g \right) }+{ 6CO }_{ 2\left( g \right) }$$ Given
$$ \triangle { G }^{ o }=2879kJ{ mol }^{ -1 }$$
$$ \triangle { S }^{ o }=-205Jk^{-1}{ mol }^{ -1 }$$
Calculate the electron gain enthalpy of fluorine from the data given below. $$\Delta H_f$$ of KF is - 560.8 KJ/ mol, dissociation energy of $$F_2$$ is 158.9 KJ / mol. Lattice energy of KF is 807.5 KJ/mol, ionization energy of potassium is 414.2 KJ/mol and enthalpy of sublimation of $$K = 87.8 KJ/ mol.$$
If the molar heat capacity of $$O_2$$ gas is $$640Jk^{-1}mol^{-1}$$. Then calculate its specific heat capacity.
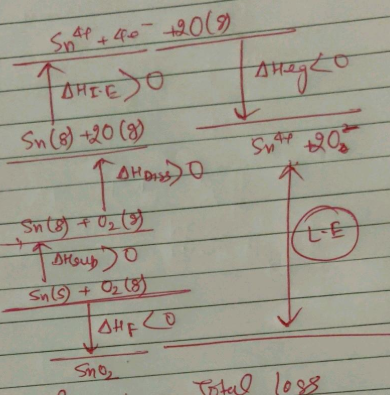
Calculate $$\Delta H_{lattice} $$ of $$SnO_2$$, If $$\Delta H_f$$ of $$SnO_2$$ is -588 KJ / mol, Enthalpy of Sublimation (Sn) = 292 KJ / mol, Enthalpy of Dissociation $$(O_2) = 454 \, KJ / mol$$. Total Electron gain enthalpy for O = 636 KJ / mol, Ionization enthalpy $$(Sn \rightarrow Sn^{4+})$$ = 8990 kJ / mol.
Total gain = Total loss
$$\Delta H_{I.E} + \Delta H_{ss} + \Delta H_{sub} = |\Delta H_F| + |\Delta H_{eg} | + L. E$$
$$\Rightarrow 8990 + 454 + 292 = 588 + 636 + L.E. $$
$$L.E = 11596 KJ$$
$$\Delta H_{I.E} + \Delta H_{ss} + \Delta H_{sub} = |\Delta H_F| + |\Delta H_{eg} | + L. E$$
$$\Rightarrow 8990 + 454 + 292 = 588 + 636 + L.E. $$
$$L.E = 11596 KJ$$
A gas expands from 14 liters to 19 liters against a constant pressure of 2 atm. During the process 600 J of heat flows in the gas from the surroundings. Calculate the internal energy change of its system.
Calculate w and $$\Delta U$$ for the conversion of 0.5 mol of water at 100-degree celsius to steam at 1atm pressure. The heat of vaporization of water at 100degree celsius is 40670 J/mol.
During an adiabatic process, the pressure of a gas is found to be proportional to cube of its absolute temperature. Calculate the Poisson's ratio of gas.
Work done by a sample of an ideal gas in a process A double the work done in another process B. The temperature rises through the same amount in the two processes. If $${C_A}$$ and $${C_B}$$ are the molar heat capacities for the two processes, then the relation between $$C_A$$ and $$C_B$$ will be:
Calculate $$\Delta U$$ and $$\Delta H$$ in calories if 1 mole of a monoatomic ideal gas is heated at constant pressure of 1 atm from $$25^oC$$ to $$50^oC$$.
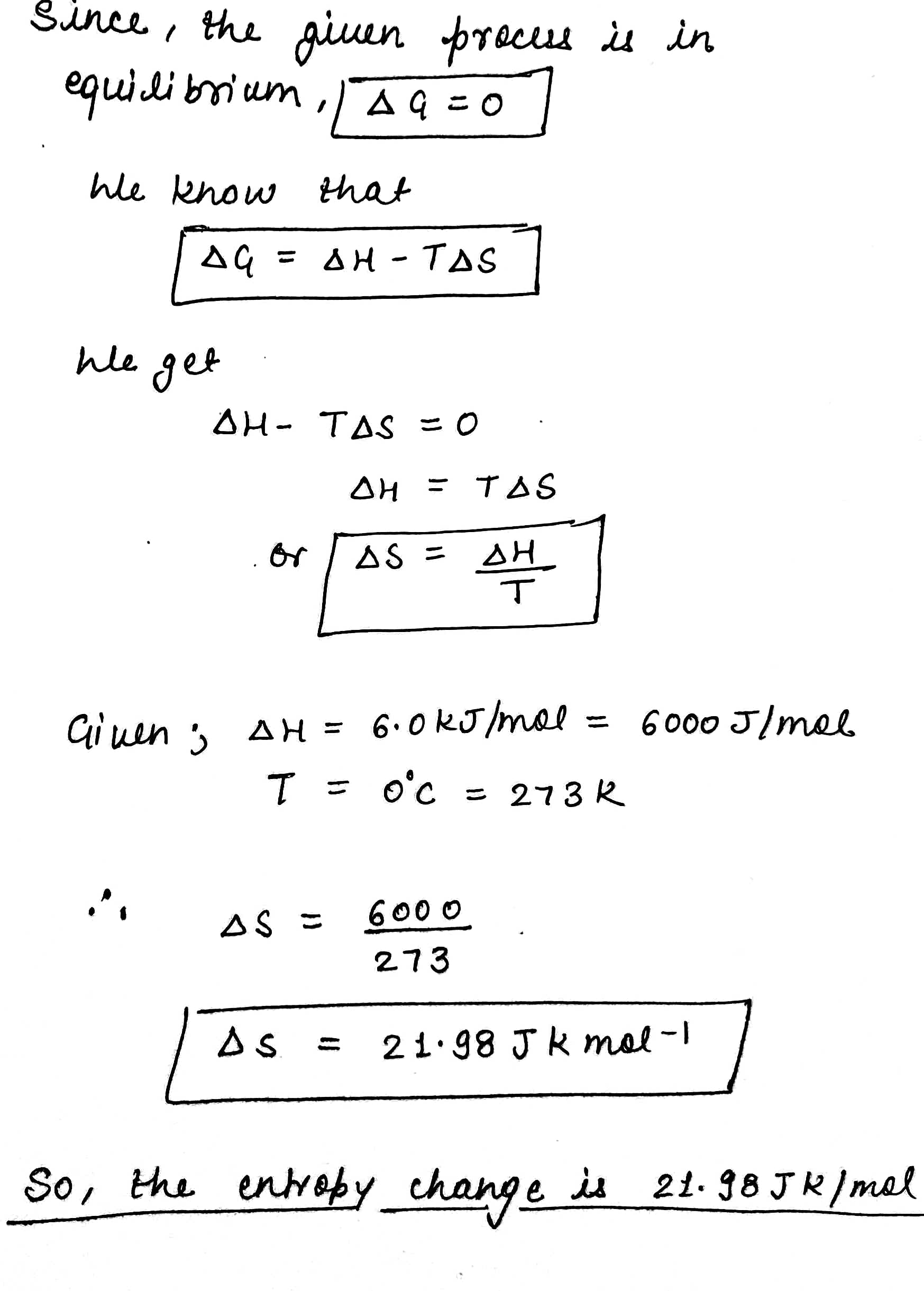
At $$O^oC$$ ice and water are in equilibrium and enthalpy change for the process:
$${ H }_{ 2 }{ O }_{ (S) }\rightleftharpoons { H }_{ 2 }{ O\quad (l) }$$ is 6.0 kJ $$mol^{-1}$$
Calculate the entropy change for this conversion of ice into liquid water.
An athlete in the weight room lifts a $$50kg$$ mass through a vertical distance of $$2.0m$$. The mass is allowed to fall through the $$2.0m$$ distance while coupled to an electrical generator. The electrical generator produces an equal amount of electrical work which is used to produce aluminium by Hall electrolytic process.
$${ Al }_{ 2 }{ O }_{ 3 }(\textrm{solution})+3C(\textrm{graphite})\rightarrow 2Al(l)+3CO(g);\Delta { G }^{ o }=593kJ$$
How many times must the athlete lift the $$50kg$$ mass to provide sufficient Gibbs energy to produce $$27g$$ $$Al$$? $$\left( g=10m/{ s }^{ 2 } \right) $$
$${ Al }_{ 2 }{ O }_{ 3 }(\textrm{solution})+3C(\textrm{graphite})\rightarrow 2Al(l)+3CO(g);\Delta { G }^{ o }=593kJ$$
How many times must the athlete lift the $$50kg$$ mass to provide sufficient Gibbs energy to produce $$27g$$ $$Al$$? $$\left( g=10m/{ s }^{ 2 } \right) $$
The increase in Gibbs free energy (in kJ) of $$13g$$ of ethanol (density $$=0.78g{cm}^{-3}$$), when the pressure is increased isothermally from $$1$$ bar to $$3001$$ bar, is _____.
State and explain Hess's law of constant heat summation.
Hess's law of constant heat of summation states that regardless of the multiple stages or steps of a reaction the total enthalpy change of the reaction is the sum of all changes.
For $$R\rightarrow P$$;
$$\Delta H_r=\Delta H_1+\Delta H_2+\Delta H_3$$.
The first ionisation enthalpy of Li is 5.4 eV and the electron gain enthalpy of Cl is 3.6 eV. Calculate $$ \triangle H $$ in kcal mol$$^{-1} $$ for the reaction,
$$ Li(g) +Cl(g) \rightarrow Li^++ Cl^- $$
Carried out at such low pressure that resulting ions do not combine with each other.
Explain the term lattice energy as applied to an ionic solid. Calculate the lattic energy of caesium chloride using the following data:
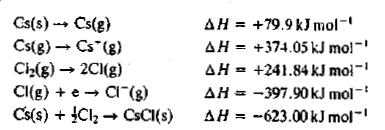
Ammonium nitrate can decompose with explosion by the following reaction :
$$NH_{4}NO_{3(s)}\rightarrow N_{2}O_{(g)} + 2H_2O_{(g)}; \, \Delta H = -37.0\ kJ$$
Calculate the heat produced when $$2.50\ g$$ of $$NH_{4}NO_{3}$$ decomposes.
A cooking gas cylinder is assumed to contain $$11.2 \ kg$$ isobutane. The combustion of isobutane is given by:
$$C_{4}H_{10(g)} + (13/ 2)O_{2(g)} \rightarrow 4CO_{2(g)} + 5H_{2}O_{(l)} ; \Delta H = -2658\ kJ$$
(a) If a family needs $$15000\ kJ$$ of energy per day for cooking, how long would the cylinder last?
(b) Assuming that $$30\%$$ of the gas is wasted due to incomplete combustion, how long would the cylinder last?
$$C_{4}H_{10(g)} + (13/ 2)O_{2(g)} \rightarrow 4CO_{2(g)} + 5H_{2}O_{(l)} ; \Delta H = -2658\ kJ$$
(a) If a family needs $$15000\ kJ$$ of energy per day for cooking, how long would the cylinder last?
(b) Assuming that $$30\%$$ of the gas is wasted due to incomplete combustion, how long would the cylinder last?
For the reaction, $$C(s) +O_2(g) \rightarrow CO_2(g),$$ $$\Delta H ^{\circ}=-393.51\ kJ/mol$$ and $$\Delta S ^{\circ}=2.86\ J/mol. K$$ at $$25^{\circ}C$$. Does the reaction become more or less favourable as the temperature increases?
Show how the Born-Haber cycle may be used to estimate the enthalpy of the hypothetical reaction:
$$Ca(s)+ Cl_2(g)\to CaCl(s)$$
explain why $$CaCl(s)$$ has never been made even though the enthalpy for this reaction is negative.
Calculate $$\Delta G^0$$ for the following reaction.
$$Ag^+(aq)+Cl^-(aq)\rightarrow AgCl(s)$$
Given: $$\Delta G^0_f(AgCl)=-109$$ kJ/mol
$$\Delta G^0_f(Cl^-)=-129$$ kJ/mol
$$\Delta G^0_f(Ag^+)=77$$ kJ/mol
Represent the given reaction in the form of a cell. Also calculate $$E^0$$ of the cell and find $$log K_{sp}$$ of $$AgCl$$.
What is the relationship between $$\Delta G, \Delta H \ \& \ \Delta S$$?
From the following data of AH, of the following reactions,$$C_{( s)}+\dfrac{1}{2}O_2(g) \longrightarrow CO_{(g)}$$; $$\Delta H = -110 \ kJA$$ $$C_{(s)} + H_2O_{(g)} \longrightarrow CO_{(g)} + H_{2(g)}; \Delta H = 132kJ$$
Calculate the mole composition of the mixture of steam and oxygen on being passed over coke at $$1273\ K$$, keeping the temperature constant.
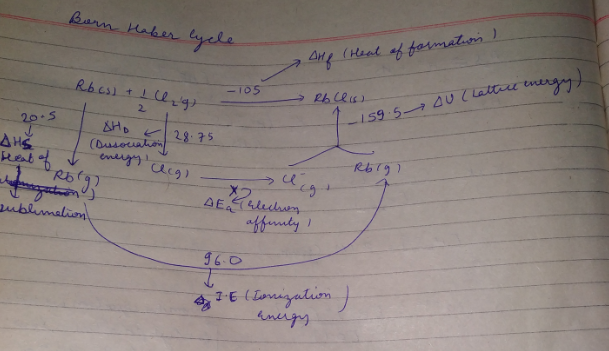
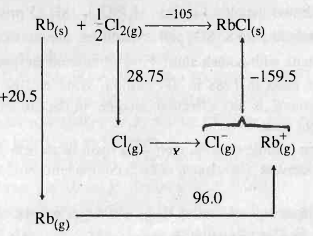
The Born-Haber's cycle for rubidium chloride $$ (RbCl) $$ is given above , ( the energies are in $$ kcal \,mol^{-1} $$.
Find out the electron affinity of chloride in $$ kJ\,mol^{-1} $$ .
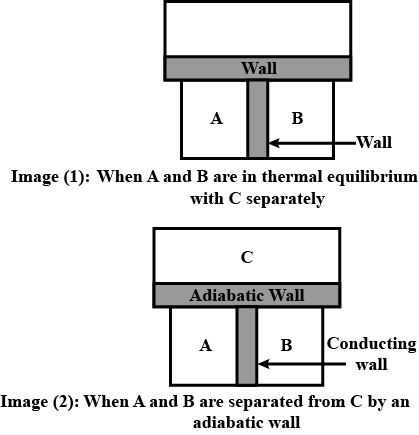
What is Heat capacity?
How non-spotaneous process be converted to spontaneous process?
At $$ 0^o $$ and $$ 1 atm, $$ heat absorbed by the system by melting of one mle of ice is $$ 6.05 KJ/mol. $$ The molar volume of ice and water are $$ 0.0196 L $$ and $$ 0.0180 L $$ respectively. Calculate $$ \Delta H $$ and $$ \Delta U. $$
Taking a specific example show that $$\Delta S_{total}$$ is a criterion for spontaneity of a change.
State and illustrate Hess's law.
What you mean by Born-Haber cycle ?
What is Thermodynamics? Explain the Zeroth law of Thermodynamics and give its importance.
It is based on the principle of temperature.
To understand this law, consider two systems $$A$$ and $$B$$, separated by an adiabatic wall, each of these are in contact with a third system $$C$$ by a conducting wall. The states of the system will change until $$A$$ and $$B$$ are in equilibrium with $$C$$. Now, let the adiabatic wall between $$A$$ and $$B$$ be replaced by a conducting wall and $$C$$ is insulated from $$A$$ and $$B$$ by an adiabatic wall. It is found that $$A$$ and $$B$$ are in thermal equilibrium with each other. This is the basis of Zeroth law of thermodynamics. This law states that the two systems are in thermal equilibrium with a third system separately, then both are in thermal equilibrium with each other.
The zeroth law apparently suggests that when two systems $$A$$ and $$B$$ are in thermal equilibrium, then , there must be a physical quantity that has the same value for both. The thermodynamic variable whose value is equal for the two systems (in thermal equilibrium) is called temperature $$(T)$$. If $$A$$ and $$B$$ are separately in equilibrium with $$C$$, then, $$T_A=T_C$$ and $$T_B=T_C-$$ This means that $$T_A=T_B$$. So, the systems $$A$$ and $$B$$ are in thermal equilibrium.
To understand this law, consider two systems $$A$$ and $$B$$, separated by an adiabatic wall, each of these are in contact with a third system $$C$$ by a conducting wall. The states of the system will change until $$A$$ and $$B$$ are in equilibrium with $$C$$. Now, let the adiabatic wall between $$A$$ and $$B$$ be replaced by a conducting wall and $$C$$ is insulated from $$A$$ and $$B$$ by an adiabatic wall. It is found that $$A$$ and $$B$$ are in thermal equilibrium with each other. This is the basis of Zeroth law of thermodynamics. This law states that the two systems are in thermal equilibrium with a third system separately, then both are in thermal equilibrium with each other.
The zeroth law apparently suggests that when two systems $$A$$ and $$B$$ are in thermal equilibrium, then , there must be a physical quantity that has the same value for both. The thermodynamic variable whose value is equal for the two systems (in thermal equilibrium) is called temperature $$(T)$$. If $$A$$ and $$B$$ are separately in equilibrium with $$C$$, then, $$T_A=T_C$$ and $$T_B=T_C-$$ This means that $$T_A=T_B$$. So, the systems $$A$$ and $$B$$ are in thermal equilibrium.
Enthalpies of formation of $$ CO(g),CO_2(g), NaO(g) $$ and $$ N_2O_4(g) $$ are $$ -110,-393.81$$ and $$ 9.7 kJ \quad mol^{-1} $$ respectively. Find the value of $$ \Delta H $$ for the reaction
$$ N_2O_{3(g)} \rightarrow N_2O_{(g)}+3CO_{(g)} $$
For the reaction
$$ 2A_{(g)}+B_{(g)} \rightarrow 2D_{(g)} $$
$$ \Delta U^o =-10.5 kJ $$ and $$ \Delta S^o =-44.1 JK_{-1} $$
Calculate $$ \Delta G^o $$ for the reaction and predict whether the reaction may occur spontaneously.
The reaction of cyanamide, $$ NH_2CN(s), $$ with dioxygen was carried out in a bomb clorimeter, and $$ \Delta U $$ was found to be $$ -742.7 kJ mol^{-1} $$ at $$ 298 K. $$ Calculate enthalpy change for the reaction at
$$ 298 K. NH_2CN(g) + 3/2O_2(g) \rightarrow N_2(g)+CO_2(g)+H_2O(l) $$
Explain heat, work and internal energy of a system.
A chemist while studying the properties of gaseous $$CCl_2F_2$$, a chlorofluorocarbon refrigerant cooled a $$1.25\ g$$ sample at constant atmospheric pressure of $$1.0\ atm$$ from $$320\ K$$ to $$293\ K$$. During cooling, the sample volume decreased from $$274$$ to $$248\ mL$$. Calculate $$\Delta H$$ and $$\Delta U$$ for the chorofluorocarbon for this process. For $$CCl_2F_2, C_p \simeq 80.7\ J/(mol\ K)$$.
In a gobar gas plant, gobar gas is obtained by bacterial fermentation of animal refuse. The main combination gas present in the gobar gas is found to be methane ($$80\%$$ by weight )whose heat of combustion is $$809\ mol^{-1}$$. How much gobar gas would have to produced per day for a village of $$100$$ families if average consumption of a family is $$20.000\ kJ$$ per day to meet all its energy requirements.
Class 11 Medical Chemistry Extra Questions
- Chemical Bonding And Molecular Structure Extra Questions
- Classification Of Elements And Periodicity In Properties Extra Questions
- Environmental Chemistry Extra Questions
- Equilibrium Extra Questions
- Hydrocarbons Extra Questions
- Hydrogen Extra Questions
- Organic Chemistry Some Basic Principles And Techniques Extra Questions
- Redox Reactions Extra Questions
- Some Basic Concepts Of Chemistry Extra Questions
- States Of Matter Gases And Liquids Extra Questions
- Structure Of Atom Extra Questions
- The P-Block Elements Extra Questions
- Thermodynamics Extra Questions
- The S-Block Elements Extra Questions